# Análisis Exploratorio de Datos (EDA) Semestre 01, 2026 ## Definición El Análisis Exploratorio de Datos (EDA) es el proceso inicial de análisis de los datos utilizando estadística. Busca: * Entender la estructura del conjunto de datos * Resumir sus características principales * Detectar patrones, anomalías, valores atípicos y/o valores faltantes * Formular hipótesis ## Importancia * Mal EDA → malos modelos * Buen EDA → mejores decisiones EDA permite: * Detectar errores de medición * Identificar variables irrelevantes * Entender relaciones entre variables ## Minería de Datos 1. Comprensión del problema 2. Comprensión de los datos 3. **Análisis Exploratorio de Datos** 📍 4. Limpieza y transformación 5. Modelado 6. Evaluación ## Tipos de análisis exploratorio Dependiendo del número de variables que se analizan: * **Análisis Univariado**: una variable * **Análisis Bivariado**: dos variables * **Análisis Multivariado**: más de dos variables Pero... también depende del **tipo de variable**. ## Tipos de variables Antes de analizar, debemos clasificar las variables. ### Variables Cualitativas * Nominales (ej. género, color, país) * Ordinales (ej. nivel educativo, satisfacción) ### Variables Cuantitativas * Discretas (ej. número de hijos) * Continuas (ej. peso, edad, ingresos) 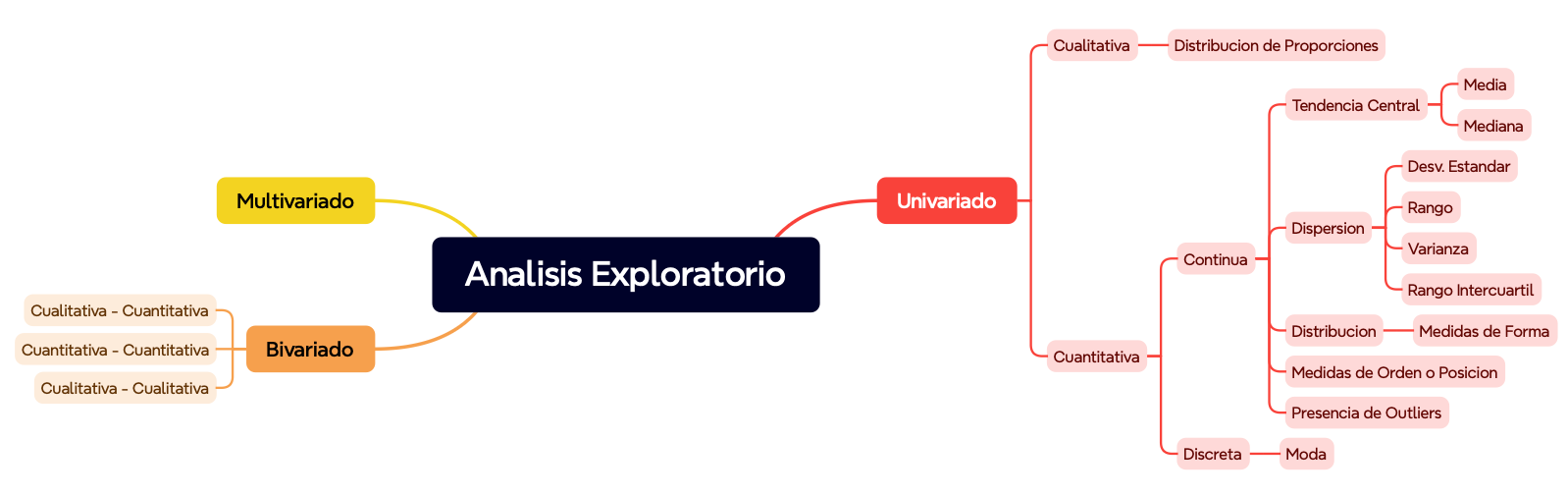 ## Análisis Univariado Analiza una sola variable a la vez. Objetivos: * Entender su distribución * Identificar valores típicos * Detectar valores atípicos Se divide según el tipo de variable. ### Univariado – Variable Cualitativa Nos interesa: * Distribución de proporciones * Categorías más frecuentes Preguntas típicas: * ¿Qué categoría aparece más? * ¿Existen categorías raras o poco frecuentes? Herramientas comunes: * Tablas de frecuencia * Gráficos de barras ### Univariado – Variable Cuantitativa Continua Medidas de tendencia central: * Media * Mediana Medidas de dispersión: * Desviación estándar * Varianza * Rango * Rango intercuartil ### Univariado – Forma de la distribución Además del centro y la dispersión, analizamos: * Simetría * Asimetría * Curtosis Esto nos ayuda a entender: * Si la media es representativa * Si existen colas largas ### Univariado – Medidas de posición Permiten ubicar observaciones dentro de la distribución: * Cuartiles * Percentiles Sirven para: * Comparaciones * Detección de outliers ### Univariado – Outliers Los outliers son valores inusuales. Indican: * Errores de medición * Casos extremos reales No siempre deben eliminarse!!! ## Análisis Bivariado Analiza la relación entre dos variables. El tipo de análisis depende de: * Cualitativa – Cuantitativa * Cuantitativa – Cuantitativa * Cualitativa – Cualitativa ### Bivariado – Cualitativa vs Cuantitativa Pregunta típica: * ¿Cómo cambia una variable numérica entre categorías? Ejemplos: * Salario según nivel educativo * Edad según tipo de cliente Herramientas comunes: * Boxplots * Resúmenes por grupo ### Bivariado – Cuantitativa vs Cuantitativa Pregunta típica: * ¿Existe relación entre ambas variables? Nos interesa: * Dirección de la relación * Intensidad * Forma Herramientas comunes: * Diagramas de dispersión * Correlación ### Bivariado – Cualitativa vs Cualitativa Pregunta típica: * ¿Existe asociación entre categorías? Ejemplos: * Género vs tipo de compra * Carrera vs aprobación Herramientas comunes: * Tablas de contingencia * Proporciones condicionadas ## Normalidad de los datos En el Análisis Exploratorio de Datos es importante evaluar si las variables cuantitativas siguen una distribución normal. La normalidad es relevante porque: * Muchas técnicas estadísticas asumen normalidad * Afecta la interpretación de la media y la desviación estándar * Influye en la selección de modelos y pruebas estadísticas Una variable sigue una distribución normal si: * Es simétrica respecto a la media * Tiene forma de campana * La mayoría de los valores se concentran alrededor del centro ### Evaluación de la normalidad La normalidad puede evaluarse de 2 formas: **Gráfica**: * Histogramas * Gráficos Q–Q (Quantile–Quantile) **Estadística**: * Prueba de Shapiro–Wilk * Prueba de Kolmogorov–Smirnov Si una variable no sigue una distribución normal: * Se pueden aplicar transformaciones (log, raíz cuadrada, Box-Cox) * Se pueden usar métodos no paramétricos * No necesariamente es un problema, depende del objetivo del análisis ## Análisis Multivariado Involucra **tres o más variables**. Objetivos: * Detectar patrones complejos * Reducir dimensionalidad * Explorar estructura de los datos ## Toma de decisiones * Elegir la variable respuesta * Identificar variables relevantes * Decidir si el problema es: * Clasificación * Regresión * Clustering